Quantum mechanics
|
WikiDoc Resources for Quantum mechanics |
|
Articles |
|---|
|
Most recent articles on Quantum mechanics Most cited articles on Quantum mechanics |
|
Media |
|
Powerpoint slides on Quantum mechanics |
|
Evidence Based Medicine |
|
Cochrane Collaboration on Quantum mechanics |
|
Clinical Trials |
|
Ongoing Trials on Quantum mechanics at Clinical Trials.gov Trial results on Quantum mechanics Clinical Trials on Quantum mechanics at Google
|
|
Guidelines / Policies / Govt |
|
US National Guidelines Clearinghouse on Quantum mechanics NICE Guidance on Quantum mechanics
|
|
Books |
|
News |
|
Commentary |
|
Definitions |
|
Patient Resources / Community |
|
Patient resources on Quantum mechanics Discussion groups on Quantum mechanics Patient Handouts on Quantum mechanics Directions to Hospitals Treating Quantum mechanics Risk calculators and risk factors for Quantum mechanics
|
|
Healthcare Provider Resources |
|
Causes & Risk Factors for Quantum mechanics |
|
Continuing Medical Education (CME) |
|
International |
|
|
|
Business |
|
Experimental / Informatics |
Overview
In physics, quantum mechanics is the study of the relationship between energy quanta (radiation) and matter, in particular that between valence shell electrons and photons. Quantum mechanics is a fundamental branch of physics with wide applications in both experimental and theoretical physics. Quantum theory generalizes all classical theories, including mechanics, electromagnetism (except general relativity), and provides accurate descriptions for many previously unexplained phenomena such as black body radiation and stable electron orbits.The effects of quantum mechanics are typically not observable on macroscopic scales, but become evident at the atomic and subatomic level.
Overview
The word “quantum” (Latin, “how much”) in quantum mechanics refers to a discrete unit that quantum theory assigns to certain physical quantities, such as the energy of an atom at rest (see Figure 1, at right). The discovery that waves have discrete energy packets (called quanta) that behave in a manner similar to particles led to the branch of physics that deals with atomic and subatomic systems which we today call quantum mechanics. It is the underlying mathematical framework of many fields of physics and chemistry, including condensed matter physics, solid-state physics, atomic physics, molecular physics, computational chemistry, quantum chemistry, particle physics, and nuclear physics. The foundations of quantum mechanics were established during the first half of the twentieth century by Albert Einstein, Werner Heisenberg, Max Planck, Louis de Broglie, Niels Bohr, Erwin Schrödinger, Max Born, John von Neumann, Paul Dirac, Wolfgang Pauli and others. Some fundamental aspects of the theory are still actively studied.
It is currently necessary to use quantum mechanics to understand the behavior of systems at atomic length scales and smaller. For example, if Newtonian mechanics governed the workings of an atom, electrons would rapidly travel towards and collide with the nucleus. However, in the natural world the electrons normally remain in an unknown orbital path around the nucleus, defying classical electromagnetism.
Quantum mechanics was initially developed to provide a better explanation of the atom, especially the spectra of light emitted by different atomic species. The quantum theory of the atom developed as an explanation for the electron's staying in its orbital, which could not be explained by Newton's laws of motion and by Maxwell's laws of classical electromagnetism.
In the formalism of quantum mechanics, the state of a system at a given time is described by a complex wave function (sometimes referred to as orbitals in the case of atomic electrons), and more generally, elements of a complex vector space. This abstract mathematical object allows for the calculation of probabilities of outcomes of concrete experiments. For example, it allows one to compute the probability of finding an electron in a particular region around the nucleus at a particular time. Contrary to classical mechanics, one can never make simultaneous predictions of conjugate variables, such as position and momentum, with arbitrary accuracy. For instance, electrons may be considered to be located somewhere within a region of space, but with their exact positions being unknown. Contours of constant probability, often referred to as “clouds” may be drawn around the nucleus of an atom to conceptualize where the electron might be located with the most probability. It should be stressed that the electron itself is not spread out over such cloud regions. It is either in a particular region of space, or it is not [citation needed]. Heisenberg's uncertainty principle quantifies the inability to precisely locate the particle.
The other exemplar that led to quantum mechanics was the study of electromagnetic waves such as light. When it was found in 1900 by Max Planck that the energy of waves could be described as consisting of small packets or quanta, Albert Einstein exploited this idea to show that an electromagnetic wave such as light could be described by a particle called the photon with a discrete energy dependent on its frequency. This led to a theory of unity between subatomic particles and electromagnetic waves called wave–particle duality in which particles and waves were neither one nor the other, but had certain properties of both. While quantum mechanics describes the world of the very small, it also is needed to explain certain “macroscopic quantum systems” such as superconductors and superfluids.
Broadly speaking, quantum mechanics incorporates four classes of phenomena that classical physics cannot account for: (i) the quantization (discretization) of certain physical quantities, (ii) wave-particle duality, (iii) the uncertainty principle, and (iv) quantum entanglement. Each of these phenomena is described in detail in subsequent sections.
History
The history of quantum mechanics began essentially with the 1838 discovery of cathode rays by Michael Faraday, the 1859 statement of the black body radiation problem by Gustav Kirchhoff, the 1877 suggestion by Ludwig Boltzmann that the energy states of a physical system could be discrete, and the 1900 quantum hypothesis by Max Planck that any energy is radiated and absorbed in quantities divisible by discrete ‘energy elements’ ε such that each of these energy elements is proportional to the frequency ν with which they each individually radiate energy, as defined by the following formula:
- <math> \epsilon = h \nu \, </math>
where h is Planck's Action Constant. Although Planck insisted that this was simply an aspect of the absorption and radiation of energy and had nothing to do with the physical reality of the energy itself, in 1905, to explain the photoelectric effect (1839), i.e. that shining light on certain materials can function to eject electrons from the material, Albert Einstein postulated, as based on Planck’s quantum hypothesis, that light itself consists of individual quanta, which later came to be called photons (1926). From Einstein's simple postulation was borne a flurry of debating, theorizing and testing, and thus, the entire field of quantum physics.
Relativity and quantum mechanics
The modern world of physics is notably founded on two tested and demonstrably sound theories of general relativity and quantum mechanics —theories which appear to contradict one another. The defining postulates of both Einstein's theory of relativity and quantum theory are indisputably supported by rigorous and repeated empirical evidence. However, while they do not directly contradict each other theoretically (at least with regard to primary claims), they are resistant to being incorporated within one cohesive model.
Einstein himself is well known for rejecting some of the claims of quantum mechanics. While clearly inventive in this field, he did not accept the more philosophic consequences and interpretations of quantum mechanics, such as the lack of deterministic causality and the assertion that a single subatomic particle can occupy numerous areas of space at one time. He also was the first to notice some of the apparently exotic consequences of entanglement and used them to formulate the Einstein-Podolsky-Rosen paradox, in the hope of showing that quantum mechanics has unacceptable implications. This was 1935, but in 1964 it was shown by John Bell (see Bell inequality) that Einstein's assumption that quantum mechanics is correct, but has to be completed by hidden variables, was based on wrong philosophical assumptions: according to the paper of J. Bell and the Copenhagen interpretation (the common interpretation of quantum mechanics by physicists, since decades), and contrary to Einstein's ideas, quantum mechanics is
- neither a "realistic" theory (since quantum measurements do not state pre-existing properties, but rather they prepare properties)
- nor a local theory (essentially not, because the state vector <math>|\psi\rangle </math> determines simultaneously the probability amplitudes at all sites, <math>|\psi\rangle\to\psi(\mathbf r), \forall \mathbf r</math>).
The Einstein-Podolsky- Rosen paradox shows in any case that there exist experiments by which one can measure the state of one particle and instantaneously change the state of its entangled partner, although the two particles can be an arbitrary distance apart; however, this effect does not violate causality, since no transfer of information happens. These experiments are the basis of some of the most topical applications of the theory, quantum cryptography, which works well, although at small distances of typically <math> {\le} </math> 100 km, being on the market since 2004.
There do exist quantum theories which incorporate special relativity—for example, quantum electrodynamics (QED), which is currently the most accurately tested physical theory [1]—and these lie at the very heart of modern particle physics. Gravity is negligible in many areas of particle physics, so that unification between general relativity and quantum mechanics is not an urgent issue in those applications. However, the lack of a correct theory of quantum gravity is an important issue in cosmology.
Attempts at a unified theory
Inconsistencies arise when one tries to join the quantum laws with general relativity, a more elaborate description of spacetime which incorporates gravitation. Resolving these inconsistencies has been a major goal of twentieth- and twenty-first-century physics. Many prominent physicists, including Stephen Hawking, have labored in the attempt to discover a "Grand Unification Theory" that combines not only different models of subatomic physics, but also derives the universe's four forces—the strong force, electromagnetism, weak force, and gravity— from a single force or phenomenon.
Quantum mechanics and classical physics
Predictions of quantum mechanics have been verified experimentally to a very high degree of accuracy. Thus, the current logic of correspondence principle between classical and quantum mechanics is that all objects obey laws of quantum mechanics, and classical mechanics is just a quantum mechanics of large systems (or a statistical quantum mechanics of a large collection of particles). Laws of classical mechanics thus follow from laws of quantum mechanics at the limit of large systems or large quantum numbers.
Main differences between classical and quantum theories have already been mentioned above in the remarks on the Einstein-Podolsky-Rosen paradox. Essentially the difference boils down to the statement that quantum mechanics is coherent (addition of amplitudes), whereas classical theories are incoherent (addition of intensities). Thus, such quantities as coherence lengths and coherence times come into play. For microscopic bodies the extension of the system is certainly much smaller than the coherence length; for macroscopic bodies one expects that it should be the other way round.
This is in accordance with the following observations:
Many “macroscopic” properties of “classic” systems are direct consequences of quantum behavior of its parts. For example, stability of bulk matter (which consists of atoms and molecules which would quickly collapse under electric forces alone), rigidity of this matter, mechanical, thermal, chemical, optical and magnetic properties of this matter—they are all results of interaction of electric charges under the rules of quantum mechanics.
Because seemingly exotic behavior of matter posited by quantum mechanics and relativity theory become more apparent when dealing with extremely fast-moving or extremely tiny particles, the laws of classical “Newtonian” physics still remain accurate in predicting the behavior of surrounding (“large”) objects—of the order of the size of large molecules and bigger.
Despite the proposal of many novel ideas, the unification of quantum mechanics—which reigns in the domain of the very small—and general relativity—a superb description of the very large—remains, tantalizingly, a future possibility. (See quantum gravity, string theory.)
Theory
There are numerous mathematically equivalent formulations of quantum mechanics. One of the oldest and most commonly used formulations is the transformation theory proposed by Cambridge theoretical physicist Paul Dirac, which unifies and generalizes the two earliest formulations of quantum mechanics, matrix mechanics (invented by Werner Heisenberg)[2] and wave mechanics (invented by Erwin Schrödinger).
In this formulation, the instantaneous state of a quantum system encodes the probabilities of its measurable properties, or "observables". Examples of observables include energy, position, momentum, and angular momentum. Observables can be either continuous (e.g., the position of a particle) or discrete (e.g., the energy of an electron bound to a hydrogen atom).
Generally, quantum mechanics does not assign definite values to observables. Instead, it makes predictions about probability distributions; that is, the probability of obtaining each of the possible outcomes from measuring an observable. Naturally, these probabilities will depend on the quantum state at the instant of the measurement. There are, however, certain states that are associated with a definite value of a particular observable. These are known as "eigenstates" of the observable ("eigen" can be roughly translated from German as inherent or as a characteristic). In the everyday world, it is natural and intuitive to think of everything being in an eigenstate of every observable. Everything appears to have a definite position, a definite momentum, and a definite time of occurrence. However, quantum mechanics does not pinpoint the exact values for the position or momentum of a certain particle in a given space in a finite time; rather, it only provides a range of probabilities of where that particle might be. Therefore, it became necessary to use different words for (a) the state of something having an uncertainty relation and (b) a state that has a definite value. The latter is called the "eigenstate" of the property being measured.
For example, consider a free particle. In quantum mechanics, there is wave-particle duality so the properties of the particle can be described as a wave. Therefore, its quantum state can be represented as a wave, of arbitrary shape and extending over all of space, called a wavefunction. The position and momentum of the particle are observables. The Uncertainty Principle of quantum mechanics states that both the position and the momentum cannot simultaneously be known with infinite precision at the same time. However, one can measure just the position alone of a moving free particle creating an eigenstate of position with a wavefunction that is very large at a particular position x, and almost zero everywhere else. If one performs a position measurement on such a wavefunction, the result x will be obtained with almost 100% probability. In other words, the position of the free particle will almost be known. This is called an eigenstate of position (mathematically more precise: a generalized eigenstate (eigendistribution) ). If the particle is in an eigenstate of position then its momentum is completely unknown. An eigenstate of momentum, on the other hand, has the form of a plane wave. It can be shown that the wavelength is equal to h/p, where h is Planck's constant and p is the momentum of the eigenstate. If the particle is in an eigenstate of momentum then its position is completely blurred out.
Usually, a system will not be in an eigenstate of whatever observable we are interested in. However, if one measures the observable, the wavefunction will instantaneously be an eigenstate (or generalized eigenstate) of that observable. This process is known as wavefunction collapse. It involves expanding the system under study to include the measurement device, so that a detailed quantum calculation would no longer be feasible and a classical description must be used. If one knows the corresponding wave function at the instant before the measurement, one will be able to compute the probability of collapsing into each of the possible eigenstates. For example, the free particle in the previous example will usually have a wavefunction that is a wave packet centered around some mean position x0, neither an eigenstate of position nor of momentum. When one measures the position of the particle, it is impossible to predict with certainty the result that we will obtain. It is probable, but not certain, that it will be near x0, where the amplitude of the wave function is large. After the measurement is performed, having obtained some result x, the wave function collapses into a position eigenstate centered at x.
Wave functions can change as time progresses. An equation known as the Schrödinger equation describes how wave functions change in time, a role similar to Newton's second law in classical mechanics. The Schrödinger equation, applied to the aforementioned example of the free particle, predicts that the center of a wave packet will move through space at a constant velocity, like a classical particle with no forces acting on it. However, the wave packet will also spread out as time progresses, which means that the position becomes more uncertain. This also has the effect of turning position eigenstates (which can be thought of as infinitely sharp wave packets) into broadened wave packets that are no longer position eigenstates.
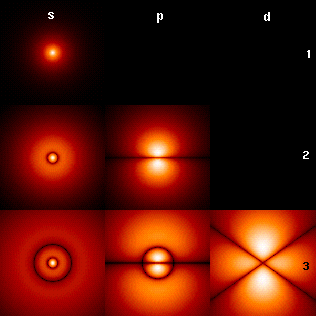
Some wave functions produce probability distributions that are constant in time. Many systems that are treated dynamically in classical mechanics are described by such "static" wave functions. For example, a single electron in an unexcited atom is pictured classically as a particle moving in a circular trajectory around the atomic nucleus, whereas in quantum mechanics it is described by a static, spherically symmetric wavefunction surrounding the nucleus (Fig. 1). (Note that only the lowest angular momentum states, labeled s, are spherically symmetric).
The time evolution of wave functions is deterministic in the sense that, given a wavefunction at an initial time, it makes a definite prediction of what the wavefunction will be at any later time. During a measurement, the change of the wavefunction into another one is not deterministic, but rather unpredictable, i.e., random.
The probabilistic nature of quantum mechanics thus stems from the act of measurement. This is one of the most difficult aspects of quantum systems to understand. It was the central topic in the famous Bohr-Einstein debates, in which the two scientists attempted to clarify these fundamental principles by way of thought experiments. In the decades after the formulation of quantum mechanics, the question of what constitutes a "measurement" has been extensively studied. Interpretations of quantum mechanics have been formulated to do away with the concept of "wavefunction collapse"; see, for example, the relative state interpretation. The basic idea is that when a quantum system interacts with a measuring apparatus, their respective wavefunctions become entangled, so that the original quantum system ceases to exist as an independent entity. For details, see the article on measurement in quantum mechanics.
Mathematical formulation
In the mathematically rigorous formulation of quantum mechanics, developed by Paul Dirac and John von Neumann, the possible states of a quantum mechanical system are represented by unit vectors (called "state vectors") residing in a complex separable Hilbert space (variously called the "state space" or the "associated Hilbert space" of the system) well defined up to a complex number of norm 1 (the phase factor). In other words, the possible states are points in the projectivization of a Hilbert space. The exact nature of this Hilbert space is dependent on the system; for example, the state space for position and momentum states is the space of square-integrable functions, while the state space for the spin of a single proton is just the product of two complex planes. Each observable is represented by a maximally-Hermitian (precisely: by a self-adjoint) linear operator acting on the state space. Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate. If the operator's spectrum is discrete, the observable can only attain those discrete eigenvalues.
The time evolution of a quantum state is described by the Schrödinger equation, in which the Hamiltonian, the operator corresponding to the total energy of the system, generates time evolution.
The inner product between two state vectors is a complex number known as a probability amplitude. During a measurement, the probability that a system collapses from a given initial state to a particular eigenstate is given by the square of the absolute value of the probability amplitudes between the initial and final states. The possible results of a measurement are the eigenvalues of the operator - which explains the choice of Hermitian operators, for which all the eigenvalues are real. We can find the probability distribution of an observable in a given state by computing the spectral decomposition of the corresponding operator. Heisenberg's uncertainty principle is represented by the statement that the operators corresponding to certain observables do not commute.
The Schrödinger equation acts on the entire probability amplitude, not merely its absolute value. Whereas the absolute value of the probability amplitude encodes information about probabilities, its phase encodes information about the interference between quantum states. This gives rise to the wave-like behavior of quantum states.
It turns out that analytic solutions of Schrödinger's equation are only available for a small number of model Hamiltonians, of which the quantum harmonic oscillator, the particle in a box, the hydrogen-molecular ion and the hydrogen atom are the most important representatives. Even the helium atom, which contains just one more electron than hydrogen, defies all attempts at a fully analytic treatment. There exist several techniques for generating approximate solutions. For instance, in the method known as perturbation theory one uses the analytic results for a simple quantum mechanical model to generate results for a more complicated model related to the simple model by, for example, the addition of a weak potential energy. Another method is the "semi-classical equation of motion" approach, which applies to systems for which quantum mechanics produces weak deviations from classical behavior. The deviations can be calculated based on the classical motion. This approach is important for the field of quantum chaos.
An alternative formulation of quantum mechanics is Feynman's path integral formulation, in which a quantum-mechanical amplitude is considered as a sum over histories between initial and final states; this is the quantum-mechanical counterpart of action principles in classical mechanics.
Interactions with other scientific theories
The fundamental rules of quantum mechanics are very broad. They assert that the state space of a system is a Hilbert space and the observables are Hermitian operators acting on that space, but do not tell us which Hilbert space or which operators, or if it even exists. These must be chosen appropriately in order to obtain a quantitative description of a quantum system. An important guide for making these choices is the correspondence principle, which states that the predictions of quantum mechanics reduce to those of classical physics when a system moves to higher energies or equivalently, larger quantum numbers. In other words, classic mechanics is simply a quantum mechanics of large systems. This "high energy" limit is known as the classical or correspondence limit. One can therefore start from an established classical model of a particular system, and attempt to guess the underlying quantum model that gives rise to the classical model in the correspondence limit
Template:Unsolved When quantum mechanics was originally formulated, it was applied to models whose correspondence limit was non-relativistic classical mechanics. For instance, the well-known model of the quantum harmonic oscillator uses an explicitly non-relativistic expression for the kinetic energy of the oscillator, and is thus a quantum version of the classical harmonic oscillator.
Early attempts to merge quantum mechanics with special relativity involved the replacement of the Schrödinger equation with a covariant equation such as the Klein-Gordon equation or the Dirac equation. While these theories were successful in explaining many experimental results, they had certain unsatisfactory qualities stemming from their neglect of the relativistic creation and annihilation of particles. A fully relativistic quantum theory required the development of quantum field theory, which applies quantization to a field rather than a fixed set of particles. The first complete quantum field theory, quantum electrodynamics, provides a fully quantum description of the electromagnetic interaction.
The full apparatus of quantum field theory is often unnecessary for describing electrodynamic systems. A simpler approach, one employed since the inception of quantum mechanics, is to treat charged particles as quantum mechanical objects being acted on by a classical electromagnetic field. For example, the elementary quantum model of the hydrogen atom describes the electric field of the hydrogen atom using a classical <math>-\frac{e^2}{4 \pi\ \epsilon_0\ } \frac{1}{r}</math> Coulomb potential. This "semi-classical" approach fails if quantum fluctuations in the electromagnetic field play an important role, such as in the emission of photons by charged particles.
Quantum field theories for the strong nuclear force and the weak nuclear force have been developed. The quantum field theory of the strong nuclear force is called quantum chromodynamics, and describes the interactions of the subnuclear particles: quarks and gluons. The weak nuclear force and the electromagnetic force were unified, in their quantized forms, into a single quantum field theory known as electroweak theory.
It has proven difficult to construct quantum models of gravity, the remaining fundamental force. Semi-classical approximations are workable, and have led to predictions such as Hawking radiation. However, the formulation of a complete theory of quantum gravity is hindered by apparent incompatibilities between general relativity, the most accurate theory of gravity currently known, and some of the fundamental assumptions of quantum theory. The resolution of these incompatibilities is an area of active research, and theories such as string theory are among the possible candidates for a future theory of quantum gravity.
Applications
Quantum mechanics has had enormous success in explaining many of the features of our world. The individual behaviour of the subatomic particles that make up all forms of matter—electrons, protons, neutrons, photons and others—can often only be satisfactorily described using quantum mechanics. Quantum mechanics has strongly influenced string theory, a candidate for a theory of everything (see reductionism). It is also related to statistical mechanics.
Quantum mechanics is important for understanding how individual atoms combine covalently to form chemicals or molecules. The application of quantum mechanics to chemistry is known as quantum chemistry. (Relativistic) quantum mechanics can in principle mathematically describe most of chemistry. Quantum mechanics can provide quantitative insight into ionic and covalent bonding processes by explicitly showing which molecules are energetically favorable to which others, and by approximately how much. Most of the calculations performed in computational chemistry rely on quantum mechanics.
Much of modern technology operates at a scale where quantum effects are significant. Examples include the laser, the transistor, the electron microscope, and magnetic resonance imaging. The study of semiconductors led to the invention of the diode and the transistor, which are indispensable for modern electronics.
Researchers are currently seeking robust methods of directly manipulating quantum states. Efforts are being made to develop quantum cryptography, which will allow guaranteed secure transmission of information. A more distant goal is the development of quantum computers, which are expected to perform certain computational tasks exponentially faster than classical computers. Another active research topic is quantum teleportation, which deals with techniques to transmit quantum states over arbitrary distances.
In many devices, even the simple light switch, quantum tunneling is vital, as otherwise the electrons in the electric current could not penetrate the potential barrier made up, in the case of the light switch, of a layer of oxide.
Philosophical consequences
- Main article: Interpretation of quantum mechanics
Since its inception, the many counter-intuitive results of quantum mechanics have provoked strong philosophical debate and many interpretations. Even fundamental issues such as Max Born's basic rules concerning probability amplitudes and probability distributions took decades to be appreciated.
The Copenhagen interpretation, due largely to the Danish theoretical physicist Niels Bohr, is the interpretation of quantum mechanics most widely accepted amongst physicists. According to it, the probabilistic nature of quantum mechanics predictions cannot be explained in terms of some other deterministic theory, and does not simply reflect our limited knowledge. Quantum mechanics provides probabilistic results because the physical universe is itself probabilistic rather than deterministic.
Albert Einstein, himself one of the founders of quantum theory, disliked this loss of determinism in measurement. (Hence his famous quote "God does not play dice with the universe.") He held that there should be a local hidden variable theory underlying quantum mechanics and consequently the present theory was incomplete. He produced a series of objections to the theory, the most famous of which has become known as the EPR paradox. John Bell showed that the EPR paradox led to experimentally testable differences between quantum mechanics and local theories. Experiments have been taken as confirming that quantum mechanics is correct and the real world must be described in terms of nonlocal theories.
The writer C.S. Lewis viewed quantum mechanics as incomplete, because notions of indeterminism did not agree with his religious beliefs.[3] Lewis, a professor of English, was of the opinion that the Heisenberg uncertainty principle was more of an epistemic limitation than an indication of ontological indeterminacy, and in this respect believed similarly to many advocates of hidden variables theories. The Bohr-Einstein debates provide a vibrant critique of the Copenhagen Interpretation from an epistemological point of view.
The Everett many-worlds interpretation, formulated in 1956, holds that all the possibilities described by quantum theory simultaneously occur in a "multiverse" composed of mostly independent parallel universes. This is not accomplished by introducing some new axiom to quantum mechanics, but on the contrary by removing the axiom of the collapse of the wave packet: All the possible consistent states of the measured system and the measuring apparatus (including the observer) are present in a real physical (not just formally mathematical, as in other interpretations) quantum superposition. (Such a superposition of consistent state combinations of different systems is called an entangled state.) While the multiverse is deterministic, we perceive non-deterministic behavior governed by probabilities, because we can observe only the universe, i.e. the consistent state contribution to the mentioned superposition, we inhabit. Everett's interpretation is perfectly consistent with John Bell's experiments and makes them intuitively understandable. However, according to the theory of quantum decoherence, the parallel universes will never be accessible for us, making them physically meaningless. This inaccessibility can be understood as follows: once a measurement is done, the measured system becomes entangled with both the physicist who measured it and a huge number of other particles, some of which are photons flying away towards the other end of the universe; in order to prove that the wave function did not collapse one would have to bring all these particles back and measure them again, together with the system that was measured originally. This is completely impractical, but even if one can theoretically do this, it would destroy any evidence that the original measurement took place (including the physicist's memory).
See also
- Interpretation of quantum mechanics
- Many-worlds interpretation
- Measurement in quantum mechanics
- Photon dynamics in the double-slit experiment
- Photon polarization
- Quantum electrochemistry
- Quantum chromodynamics
- Quantum chemistry
- Quantum computers
- Quantum electronics
- Quantum field theory
- Quantum information
- Quantum mind
- Quantum thermodynamics
- Theoretical and experimental justification for the Schrödinger equation
- Theoretical chemistry
- Quasi-set theory
- Quantum optics
References
- P. A. M. Dirac, The Principles of Quantum Mechanics (1930) -- the beginning chapters provide a very clear and comprehensible introduction
- David J. Griffiths, Introduction to Quantum Mechanics, Prentice Hall, 1995. ISBN 0-13-124405-1 -- A standard undergraduate level text written in an accessible style.
- Richard P. Feynman, Robert B. Leighton and Matthew Sands (1965). The Feynman Lectures on Physics, Addison-Wesley. Richard Feynman's original lectures (given at Caltech in early 1962) can also be downloaded as an MP3 file from www.audible.com [1]
- Hugh Everett, Relative State Formulation of Quantum Mechanics, Reviews of Modern Physics vol 29, (1957) pp 454-462.
- Bryce DeWitt, R. Neill Graham, eds, The Many-Worlds Interpretation of Quantum Mechanics, Princeton Series in Physics, Princeton University Press (1973), ISBN 0-691-08131-X
- Albert Messiah, Quantum Mechanics, English translation by G. M. Temmer of Mécanique Quantique, 1966, John Wiley and Sons, vol. I, chapter IV, section III.
- Richard P. Feynman, QED: The Strange Theory of Light and Matter -- a popular science book about quantum mechanics and quantum field theory that contains many enlightening insights that are interesting for the expert as well
- Marvin Chester, Primer of Quantum Mechanics, 1987, John Wiley, N.Y. ISBN 0-486-42878-8
- Hagen Kleinert, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 3th edition, World Scientific (Singapore, 2004) (also available online here)
- George Mackey (2004). The mathematical foundations of quantum mechanics. Dover Publications. ISBN 0-486-43517-2.
- Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 0-13-805326-X.
- Omnès, Roland (1999). Understanding Quantum Mechanics. Princeton University Press. ISBN 0-691-00435-8.
- Transnational College of Lex (1996). What is Quantum Mechanics? A Physics Adventure. Language Research Foundation, Boston. ISBN 0-9643504-1-6.
- J. von Neumann, Mathematical Foundations of Quantum Mechanics, Princeton University Press, 1955.
- H. Weyl, The Theory of Groups and Quantum Mechanics, Dover Publications 1950.
- Max Jammer, "The Conceptual Development of Quantum Mechanics" (McGraw Hill Book Co., 1966)
- Gunther Ludwig, "Wave Mechanics" (Pergamon Press, 1968) ISBN 0-08-203204-1
- Albert Messiah, Quantum Mechanics (Vol. I), English translation from French by G. M. Temmer, fourth printing 1966, North Holland, John Wiley & Sons.
- Eric R. Scerri, The Periodic Table: Its Story and Its Significance, Oxford University Press, 2006. Considers the extent to which chemistry and especially the periodic system has been reduced to quantum mechanics. ISBN 0-19-530573-6
- José Croca (2003). Towards a Nonlinear Quantum Physics. World Scientific. ISBN 981-238-210-0.
Notes
- ↑ Life on the lattice: The most accurate theory we have
- ↑ Especially since Werner Heisenberg was awarded the Nobel Prize in Physics in 1932 for the creation of quantum mechanics, the role of Max Born has been obfuscated. A 2005 biography of Born details his role as the creator of the matrix formulation of quantum mechanics. This was recognized in a paper by Heisenberg, in 1940, honoring Max Planck. See: Nancy Thorndike Greenspan, "The End of the Certain World: The Life and Science of Max Born" (Basic Books, 2005), pp. 124 - 128, and 285 - 286.
- ↑ "Does God Play Dice? Archived Lecture by Professor Steven Hawking, Department of Applied Mathematics and Theoretical Physics (DAMTP) University of Caimbridge". Retrieved 2007-09-07.
External links
| Wikiquote has quotations related to: Quantum mechanics |
Template:Wikiversity Template:Commons2
General
- The Modern Revolution in Physics - an online textbook
- J. O'Connor and E. F. Robertson: A history of quantum mechanics
- A Lazy Layman's Guide to Quantum Physics
- Introduction to Quantum Theory at Quantiki
- Quantum Physics Made Relatively Simple: three video lectures by Hans Bethe
- Getting Started with Quantum an Essay for the Uninitiated
- H is for h-bar
Course material
- MIT OpenCourseWare: Chemistry. See 5.61, 5.73, and 5.74
- MIT OpenCourseWare: Physics. See 8.04, 8.05, and 8.06
- Imperial College Quantum Mechanics Course to Download
- Spark Notes - Quantum Physics
- Lecture notes in Quantum Mechanics (comprehensive, with advanced topics)
- Quantum Physics Online : interactive introduction to quantum mechanics (RS applets)
FAQs
- Many-worlds or relative-state interpretation
- Measurement in Quantum mechanics
- A short FAQ on quantum resonances
Media
- Everything you wanted to know about the quantum world — archive of articles from New Scientist magazine.
- Quantum Physics Research From ScienceDaily
- "Quantum Trickery: Testing Einstein's Strangest Theory". The New York Times. December 27, 2005. Check date values in:
|date=(help)
Philosophy
- Quantum Mechanics (Stanford Encyclopedia of Philosophy)
- David Mermin on the future directions of physics
Template:Link FA Template:Link FA Template:Link FA
als:Quantenmechanik ar:ميكانيكا الكم bn:কোয়ান্টাম বলবিজ্ঞান zh-min-nan:Liōng-chú la̍t-ha̍k bs:Kvantna mehanika bg:Квантова механика ca:Mecànica quàntica cs:Kvantová mechanika da:Kvantemekanik de:Quantenmechanik et:Kvantmehaanika el:Κβαντική Μηχανική eo:Kvantuma mekaniko fa:مکانیک کوانتومی gl:Mecánica cuántica ko:양자역학 hr:Kvantna mehanika id:Mekanika kuantum ia:Mechanica quantic is:Skammtafræði it:Meccanica quantistica he:מכניקת הקוונטים ka:კვანტური მექანიკა la:Mechanica quantica lv:Kvantu mehānika lt:Kvantinė mechanika hu:Kvantummechanika mk:Квантна механика mr:पुंज यामिक ms:Mekanik kuantum nl:Kwantummechanica no:Kvantemekanikk nn:Kvantemekanikk sq:Mekanika kuantike simple:Quantum mechanics sk:Kvantová mechanika sl:Kvantna mehanika sr:Квантна механика sh:Kvantna mehanika fi:Kvanttimekaniikka sv:Kvantmekanik tl:Kwantum mekaniks th:กลศาสตร์ควอนตัม uk:Квантова механіка ur:مقداریہ آلاتیات wuu:量子力學 Template:WikiDoc Sources Template:WH Template:Jb1