Orbital hybridisation
Overview
In chemistry, hybridisation or hybridization is the concept of mixing atomic orbitals to form new hybrid orbitals suitable for the qualitative description of atomic bonding properties. Hybridised orbitals are very useful in the explanation of the shape of molecular orbitals for molecules. It is an integral part of valence bond theory. Although sometimes taught together with the valence shell electron-pair repulsion (VSEPR) theory, valence bond and hybridization are in fact not related to the VSEPR model.[1]
Historical development
The hybridisation theory was promoted by chemist Linus Pauling[2] in order to explain the structure of molecules such as methane (CH4). Historically, this concept was developed for such simple chemical systems but the approach was later applied more widely, and today it is considered an effective heuristic for rationalizing the structures of organic compounds.
Hybridisation theory is not as practical for quantitative calculations as Molecular Orbital Theory. Problems with hybridisation are especially notable when the d orbitals are involved in bonding, as in coordination chemistry and organometallic chemistry. Although hybridisation schemes in transition metal chemistry can be used, they are not generally as accurate.
It is important to note that orbitals are a model representation of the behavior of electrons within molecules. In the case of simple hybridisation, this approximation is based on the atomic orbitals of hydrogen. Hybridised orbitals are assumed to be mixtures of these atomic orbitals, superimposed on each other in various proportions. Hydrogen orbitals are used as a basis for simple schemes of hybridisation because it is one of the few examples of orbitals for which an exact analytic solution to its Schrödinger equation is known. These orbitals are then assumed to be slightly, but not significantly distorted in heavier atoms, like carbon, nitrogen, and oxygen. Under these assumptions is the theory of hybridisation most applicable. It must be noted, that one does not need hybridisation to describe molecules, but for molecules made up from carbon, nitrogen and oxygen (and to a lesser extent, sulfur and phosphorus) the hybridisation theory/model makes the description much easier.
The hybridisation theory finds its use mainly in organic chemistry, and mostly concerns C, N and O (and to a lesser extent P and S). Its explanation starts with the way bonding is organized in methane.
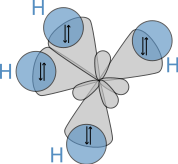
sp3 hybrids
Hybridisation describes the bonding atoms from an atom's point of view. That is, for a tetrahedrally coordinated carbon (e.g. methane, CH4), the carbon should have 4 orbitals with the correct symmetry to bond to the 4 hydrogen atoms. The problem with the existence of methane is now this: Carbon's ground-state configuration is 1s2 2s2 2px1 2py1 or perhaps more easily read:
<math>C\quad
\frac{\uparrow\downarrow}{1s}\;
\frac{\uparrow\downarrow}{2s}\;
\frac{\uparrow\,}{2p_x}\;
\frac{\uparrow\,}{2p_y}\;
\frac{\,\,}{2p_z}
</math>
(Note: The 1s orbital is lower in energy than the 2s orbital, and the 2s orbital is lower in energy than the 2p orbitals)
The valence bond theory would predict, based on the existence of two half-filled p-type orbitals (the designations px py or pz are meaningless at this point, as they do not fill in any particular order), that C forms two covalent bonds. CH2. However, methylene is a very reactive molecule (see also: carbene) and cannot exist outside of a molecular system. Therefore, this theory alone cannot explain the existence of CH4.
Furthermore, ground state orbitals cannot be used for bonding in CH4. While exciting a 2s electron into a 2p orbital would theoretically allow for four bonds according to the valence bond theory, (which has been proved experimentally correct for systems like O2) this would imply that the various bonds of CH4 would have differing energies due to differing levels of orbital overlap. Once again, this has been experimentally disproved: any hydrogen can be removed from a carbon with equal ease.
To summarise, to explain the existence of CH4 (and many other molecules) a method by which as many as 12 bonds (for transition metals) of equal strength (and therefore equal length) can be created was required.
The first step in hybridisation is the excitation of one (or more) electrons (we will have a look on the carbon atom in methane, for simplicity of the discussion):
<math> C^{*}\quad \frac{\uparrow\downarrow}{1s}\; \frac{\uparrow\,}{2s}\; \frac{\uparrow\,}{2p_x} \frac{\uparrow\,}{2p_y} \frac{\uparrow\,}{2p_z} </math>
The proton that forms the nucleus of a hydrogen atom attracts one of the valence electrons on carbon. This causes an excitation, moving a 2s electron into a 2p orbital. This, however, increases the influence of the carbon nucleus on the valence electrons by increasing the effective core potential (the amount of charge the nucleus exerts on a given electron = Charge of Core − Charge of all electrons closer to the nucleus).
The combination of these forces creates new mathematical functions known as hybridised orbitals. In the case of carbon attempting to bond with four hydrogens, four orbitals are required. Therefore, the 2s orbital (core orbitals are almost never involved in bonding) mixes with the three 2p orbitals to form four sp3 hybrids (read as s-p-three). See graphical summary below.
becomes <math> C^{*}\quad \frac{\uparrow\downarrow}{1s}\; \frac{\uparrow\,}{sp^3}\; \frac{\uparrow\,}{sp^3} \frac{\uparrow\,}{sp^3} \frac{\uparrow\,}{sp^3} </math>
In CH4, four sp3 hybridised orbitals are overlapped by hydrogen's 1s orbital, yielding four σ (sigma) bonds. The four bonds are of the same length and strength. This theory fits our requirements.
An alternative view is: View the carbon as the C4− anion. In this case all the orbitals on the carbon are filled:
<math> C^{4-}\quad \frac{\uparrow\downarrow}{1s}\; \frac{\uparrow\downarrow}{2s}\; \frac{\uparrow\downarrow}{2p_x} \frac{\uparrow\downarrow}{2p_y} \frac{\uparrow\downarrow}{2p_z} </math>
If we now recombine these orbitals with the empty s-orbitals of 4 hydrogens (4 protons, H+) and allow maximum separation between the 4 hydrogens (i.e. tetrahedral surrounding of the carbon), we see that at any orientation of the p-orbitals, a single hydrogen has an overlap of 25% with the s-orbital of the C, and a total of 75% of overlap with the 3 p-orbitals (see that the relative percentages are the same as the character of the respective orbital in an sp3-hybridisation model, 25% s- and 75% p-character).
According to the orbital hybridisation theory the valence electrons in methane should be equal in energy but its photoelectron spectrum [3] shows two bands, one at 12.7 eV (one electron pair) and one at 23 eV (three electron pairs). This apparent inconsistency can be explained when one considers additional orbital mixing taking place when the sp3 orbitals mix with the 4 hydrogen orbitals.
sp2 hybrids
Other carbon based compounds and other molecules may be explained in a similar way as methane. Take, for example, ethene (C2H4). Ethene has a double bond between the carbons. The Lewis structure looks like this:
Ethene Lewis Structure. Each C bonded to two hydrogens and one double bond between them.
Carbon will sp2 hybridise, because hybrid orbitals will form only σ bonds and one π (pi) bond is required for the double bond between the carbons. The hydrogen-carbon bonds are all of equal strength and length, which agrees with experimental data.
In sp2 hybridisation the 2s orbital is mixed with only two of the three available 2p orbitals:
<math> C^{*}\quad \frac{\uparrow\downarrow}{1s}\; \frac{\uparrow\,}{sp^2}\; \frac{\uparrow\,}{sp^2} \frac{\uparrow\,}{sp^2} \frac{\uparrow\,}{p} </math>
forming a total of 3 sp2 orbitals with one p-orbital remaining. In ethylene the two carbon atoms form a σ bond by overlapping two sp2 orbitals and each carbon atom forms two covalent bonds with hydrogen by s–sp2 overlap all with 120° angles. The π bond between the carbon atoms perpendicular to the molecular plane is formed by 2p–2p overlap.
The amount of p-character is not restricted to integer values, i.e. hybridisations like sp2.5 are also readily described. In this case the geometries are somewhat distorted from the ideally hybridised picture. For example, as stated in Bent's rule, a bond tends to have higher p-character when directed toward a more electronegative substituent.
sp hybrids
The chemical bonding in compounds such as alkynes with triple bonds is explained by sp hybridisation.
<math> C^{*}\quad \frac{\uparrow\downarrow}{1s}\; \frac{\uparrow\,}{sp}\; \frac{\uparrow\,}{sp} \frac{\uparrow\,}{p} \frac{\uparrow\,}{p} </math>
In this model the 2s orbital mixes with only one of the three p-orbitals resulting in two sp orbitals and two remaining unchanged p orbitals. The chemical bonding in acetylene (C2H2) consists of sp–sp overlap between the two carbon atoms forming a σ bond and two additional π bonds form by p–p overlap. Each carbon also bonds to hydrogen in a sigma s–sp overlap at 180° angles.
Hybridisation and molecule shape
Hybridisation, along with the VSEPR theory, helps to explain molecule shape:
- AX1 (e.g., LiH): no hybridisation; trivially linear shape
- AX2 (e.g., BeCl2): sp hybridisation; linear or diagonal shape; bond angles are cos−1(−1) = 180°
- AX3 (e.g., BCl3): sp2 hybridisation; trigonal planar shape; bond angles are cos−1(−1/2) = 120°
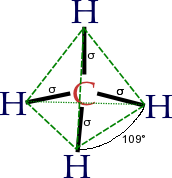
- AX4 (e.g., CCl4): sp3 hybridisation; tetrahedral shape; bond angles are cos−1(−1/3) ≈ 109.5°
- AX5 (e.g., PCl5): sp3d hybridisation; trigonal bipyramidal shape
- AX6 (e.g., SF6): sp3d2 hybridisation; octahedral (or square bipyramidal) shape
This holds if there are no lone electron pairs on the central atom. If there are, they should be counted in the Xi number, but bond angles become smaller due to increased repulsion. For example, in water (H2O), the oxygen atom has two bonds with H and two lone electron pairs (as can be seen with the valence bond theory as well from the electronic configuration of oxygen), which means there are four such 'elements' on O. The model molecule is, then, AX4: sp3 hybridisation is utilized, and the electron arrangement of H2O is tetrahedral. This agrees with the experimentally-determined shape for water, a non-linear, bent structure, with a bond angle of 104.5 degrees (the two lone-pairs are not visible).
In general, for an atom with s and p orbitals forming hybrids hi and hj with included angle <math>\theta</math>, the following holds: 1 + <math>\lambda</math>i<math>\lambda</math>j cos(<math>\theta</math>) = 0. The p-to-s ratio for hybrid i is <math>\lambda</math>i2, and for hybrid j it is <math>\lambda</math>j2. In the special case of equivalent hybrids on the same atom, again with included angle <math>\theta</math>, the equation reduces to just 1 + <math>\lambda</math>2 cos(<math>\theta</math>) = 0. For example, BH3 has a trigonal planar geometry, three 120o bond angles, three equivalent hybrids about the boron atom, and thus 1 + <math>\lambda</math>2 cos(<math>\theta</math>) = 0 becomes 1 + <math>\lambda</math>2 cos(120o) = 0, giving <math>\lambda</math>2 = 2 for the p-to-s ratio. In other words, sp2 hybrids, just as expected from the list above.
Controversy regarding d-orbital participation
Hybridisation theory has failed in a few aspects, notably in explaining the energy considerations for the involvement of d-orbitals in chemical bonding (See above for sp3d and sp3d2 hybridisation). This can be well-explained by means of an example. Consider, for instance, how the theory in question accounts for the bonding in phosphorus pentachloride (PCl5). d-orbitals are large, comparatively distant from the nucleus and high in energy. Radial distances of orbitals from the nucleus seem to reveal that d-orbitals are way too high in energy to 'mix' with s- and p-orbitals. 3s - 0.47 , 3p - 0.55, 3d - 2.4 (in angstroms). Thus, at first sight, it seems improbable for sp3d hybridisation to occur.
However, a deeper glance into the factors that affect orbital size(and energy) reveals more. Formal charge on the central atom is one such factor, and it's obvious that the P atom in PCl5 has quite a large partial positive charge on itself. Thus the 3d orbital contracts in size to enough of an extent so that hybridisation may occur with s and p orbitals. Further, note the cases in which d-orbital participation was proposed in hybridisation: SF6(sulfur hexafluoride), IF7, XeF6; in all these molecules, the central atom is surrounded by the highly electronegative fluorine atom, thus making hybridisation probable among s, p and d orbitals. A further study reveals that orbital size also depends on the number of electrons occupying it. And even further, coupling of d orbital electrons also results in contraction, albeit to a smaller extent.
The molecular orbital theory, however, offers a clearer insight into the bonding in these molecules.
Hybridisation theory vs. MO theory
Hybridisation theory is an integral part of organic chemistry and in general discussed together with molecular orbital theory in advanced organic chemistry textbooks although for different reasons. One textbook notes that for drawing reaction mechanisms sometimes a classical bonding picture is needed with 2 atoms sharing two electrons [4]. It also comments that predicting bond angles in methane with MO theory is not straightforward. Another textbook treats hybridisation theory when explaining bonding in alkenes [5] and a third [6] uses MO theory to explain bonding in hydrogen but hybridisation theory for methane.
Although the language and pictures arising from Hybridisation Theory, more widely known as Valence Bond Theory, remain widespread in synthetic organic chemistry, this qualitative analysis of bonding has been largely superseded by molecular orbital theory in other branches of chemistry. For example, inorganic chemistry texts have all but abandoned instruction of hybridisation, except as a historical footnote.[7][8] One specific problem with hybridisation is that it incorrectly predicts the photoelectron spectra of many molecules, including such fundamental species such as methane and water. From a pedagogical perspective, hybridisation approach tends to over-emphasize localization of bonding electrons and does not effectively embrace molecular symmetry as does MO Theory.
References
- ↑ "It is important to recognize that the VSEPR model provides an approach to bonding and geometry based on the Pauli principle that is completely independent of the valence bond (VB) theory or of any orbital description of bonding." Gillespie, R. J. J. Chem. Educ. 2004, 81, 298-304.
- ↑ L. Pauling, J. Am. Chem. Soc. 53 (1931), 1367
- ↑ photo electron spectrum of methane 1 photo electron spectrum of methane 2
- ↑ Organic Chemistry. Jonathan Clayden, Nick Greeves, Stuart Warren, and Peter Wothers 2001 ISBN 0-19-850346-6
- ↑ Organic Chemistry, Third Edition Marye Anne Fox James K. Whitesell 2003 ISBN 978-0-7637-3586-9
- ↑ Organic Chemistry 3rd Ed. 2001 Paula Yurkanis Bruice ISBN 0-13-017858-6
- ↑ G. L. Miessler and D. A. Tarr “Inorganic Chemistry” 3rd Ed, Pearson/Prentice Hall publisher, ISBN 0-13-035471-6.
- ↑ Shriver, D. F.; Atkins, P. W.; Overton, T. L.; Rourke, J. P.; Weller, M. T.; Armstrong, F. A. “Inorganic Chemistry” W. H. Freeman, New York, 2006. ISBN 0-7167-4878-9.
See also
External links
- Covalent Bonds and Molecular Structure
- Hybridisation flash movie
- Hybridised orbital 3D preview progam in OpenGL
cs:Hybridizace orbitalů de:Hybrid-Orbital mk:Хибридизација (хемија) nl:Hybridisatie sl:Hibridizacija sr:Хибридизација орбитала su:Hibridisasi orbital fi:Hybridisaatio (kemia) uk:Гібридизація (хімія)