Water model
In computational chemistry, classical water models are used for the simulation of water clusters, liquid water, and aqueous solutions with explicit solvent. These models use the approximations of molecular mechanics. Many different models have been proposed; they can be classified by the number of points used to define the model (atoms plus dummy sites), whether the structure is rigid or flexible, and whether the model includes polarization effects.
An alternative to the explicit water models is to use an implicit solvation model, also known as a continuum model.
Simple water models
The simplest water models treat the water molecule as rigid and rely only on non-bonded interactions. The electrostatic interaction is modeled using Coulomb's law and the dispersion and repulsion forces using the Lennard-Jones potential. The potential for models such as TIP3P and TIP4P is represented by
- <math>E_{ab} = \sum_{i} ^{on\ a} \sum_{j} ^{on\ b}
\frac {k_Cq_iq_j}{r_{ij}}
+ \frac {A}{r_{OO}^{12}}
- \frac {B}{r_{OO}^6}
</math>
where kC, the electrostatic constant, has a value of 332.1 Å·kcal/mol in the units commonly used in molecular modeling; qi are the partial charges relative to the charge of the electron; rij is the distance between two atoms or charged sites; and A and B are the Lennard-Jones parameters. The charged sites may be on the atoms or on dummy sites (such as lone pairs). In most water models, the Lennard-Jones term applies only to the interaction between the oxygen atoms.
The figure below shows the general shape of the 3- to 6-site water models. The exact geometric parameters (the OH distance and the HOH angle) vary depending on the model.
3-site
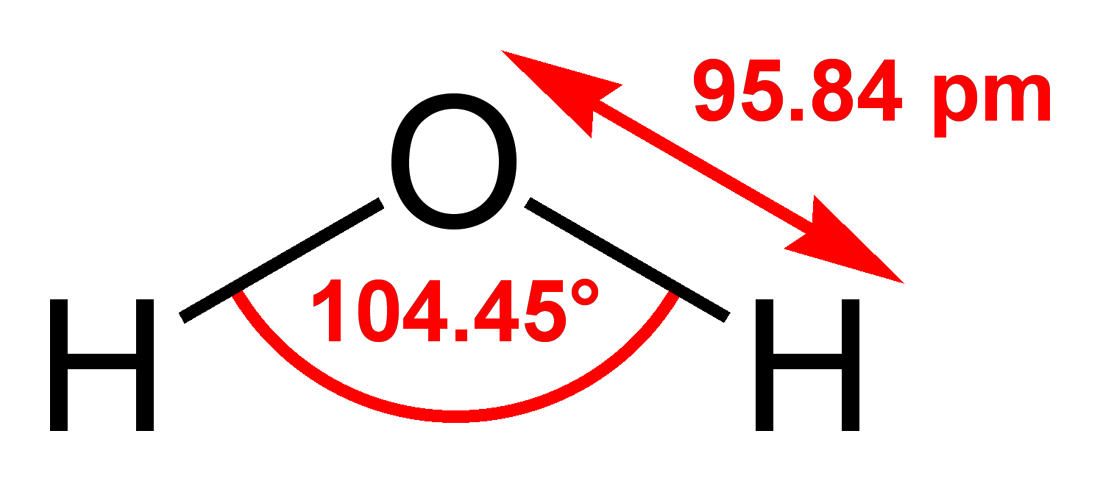
The simplest models have three interaction sites, corresponding to the three atoms of the water molecule. Each atom gets assigned a point charge, and the oxygen atom also gets the Lennard-Jones parameters. The 3-site models are very popular for molecular dynamics simulations because of their simplicity and computational efficiency. Most models use a rigid geometry matching the known geometry of the water molecule. An exception is the SPC model, which assumes an ideal tetrahedral shape (HOH angle of 109.47°) instead of the observed angle of 104.5°.
The table below lists the parameters for some 3-site models.
| TIPS[1] | SPC[2] | TIP3P[3] | SPC/E[4] | |
|---|---|---|---|---|
| r(OH), Å | 0.9572 | 1.0 | 0.9572 | 1.0 |
| HOH, deg | 104.52 | 109.47 | 104.52 | 109.47 |
| A × 10−3, kcal Å12/mol | 580.0 | 629.4 | 582.0 | 629.4 |
| B, kcal Å6/mol | 525.0 | 625.5 | 595.0 | 625.5 |
| q(O) | −0.80 | −0.82 | −0.834 | −0.8476 |
| q(H) | +0.40 | +0.41 | +0.417 | +0.4238 |
The SPC/E model adds an average polarization correction to the potential energy function:
- <math>E_{pol} = \frac 1 2 \sum_{i}
\frac {(\mu - \mu^0)^2}{\alpha_i}
</math>
where μ is the dipole of the effectively polarized water molecule (2.35 D for the SPC/E model), μ0 is the dipole moment of an isolated water molecule (1.85 D from experiment), and αi is an isotropic polarizability constant, with a value of 1.608 × 10−40 F m. Since the charges in the model are constant, this correction just results in adding 1.25 kcal/mol (5.22 kJ/mol) to the total energy. The SPC/E model results in a better density and diffusion constant than the SPC model.
The TIP3P model implemented in the CHARMM force field is a slightly modified version of the original. The difference lies in the Lennard-Jones parameters: unlike TIP3P, the CHARMM version of the model places Lennard-Jones parameters on the hydrogen atoms. The charges are not modified.[5]
Other models:
- Fergunson (flex. SPC)
- CVFF (flex.)
4-site
The 4-site models place the negative charge on a dummy atom (labeled M in the figure) placed near the oxygen along the bisector of the HOH angle. This improves the electrostatic distribution around the water molecule. The first model to use this approach was the Bernal-Fowler model published in 1933, which may also be the earliest water model. However, the BF model doesn't reproduce well the bulk properties of water, such as density and heat of vaporization, and is therefore only of historical interest. This is a consequence of the parameterization method; newer models, developed after modern computers became available, were parameterized by running Metropolis Monte Carlo or molecular dynamics simulations and adjusting the parameters until the bulk properties are reproduced well enough.
The TIP4P model, first published in 1983, is widely implemented in computational chemistry software packages and often used for the simulation of biomolecular systems. There have been subsequent reparameterizations of the TIP4P model for specific uses: the TIP4P-Ew model, for use with Ewald summation methods; the TIP4P/Ice, for simulation of solid water ice; and TIP4P/2005, a general parameterization for simulating the entire phase diagram of water.
| BF[6] | TIPS2[7] | TIP4P[3] | TIP4P-Ew[8] | TIP4P/Ice[9] | TIP4P/2005[10] | |
|---|---|---|---|---|---|---|
| r(OH), Å | 0.96 | 0.9572 | 0.9572 | 0.9572 | 0.9572 | 0.9572 |
| HOH, deg | 105.7 | 104.52 | 104.52 | 104.52 | 104.52 | 104.52 |
| r(OM), Å | 0.15 | 0.15 | 0.15 | 0.125 | 0.1577 | 0.1546 |
| A × 10−3, kcal Å12/mol | 560.4 | 695.0 | 600.0 | 656.1 | 857.9 | 731.3 |
| B, kcal Å6/mol | 837.0 | 600.0 | 610.0 | 653.5 | 850.5 | 736.0 |
| q(M) | −0.98 | −1.07 | −1.04 | −1.04844 | −1.1794 | −1.1128 |
| q(H) | +0.49 | +0.535 | +0.52 | +0.52422 | +0.5897 | +0.5564 |
Others:
- TIP4PF (flexible)
5-site
The 5-site models place the negative charge on dummy atoms (labeled L) representing the lone pairs of the oxygen atom, with a tetrahedral-like geometry. An early model of these types was the BNS model of Ben-Naim and Stillinger, proposed in 1971, soon succeeded by the ST2 model of Stillinger and Rahman in 1974. Mainly due to their higher computational cost, five-site models were not developed much until 2000, when the TIP5P model of Mahoney and Jorgensen was published. When compared with earlier models, the TIP5P model results in improvements in the geometry for the water dimer, a more "tetrahedral" water structure that better reproduces the experimental radial distribution functions from neutron diffraction, and the temperature of maximum density of water. The TIP5P-E model is a reparameterization of TIP5P for use with Ewald sums.
| BNS[11] | ST2[11] | TIP5P[12] | TIP5P-E[13] | |
|---|---|---|---|---|
| r(OH), Å | 1.0 | 1.0 | 0.9572 | 0.9572 |
| HOH, deg | 109.47 | 109.47 | 104.52 | 104.52 |
| r(OL), Å | 1.0 | 0.8 | 0.70 | 0.70 |
| LOL, deg | 109.47 | 109.47 | 109.47 | 109.47 |
| A × 10−3, kcal Å12/mol | 77.4 | 238.7 | 544.5 | 590.3 |
| B, kcal Å6/mol | 153.8 | 268.9 | 554.3 | 628.2 |
| q(L) | −0.19562 | −0.2357 | −0.241 | −0.241 |
| q(H) | +0.19562 | +0.2357 | +0.241 | +0.241 |
| RL, Å | 2.0379 | 2.0160 | ||
| RU, Å | 3.1877 | 3.1287 |
Note, however, that the BNS and ST2 models do not use Coulomb's law directly for the electrostatic terms, but a modified version that is scaled down at short distances by multiplying it by the switching function S(r):
- <math>
S(r_{ij}) = \begin{cases}
0, & \mbox{if }r_{ij} \le R_L \\
\frac{(r_{12} - R_L)^2(3R_U - R_L - 2r_{ij})}{(R_U - R_L)^2}, & \mbox{if }R_L \le r_{ij} \le R_U \\
1, & \mbox{if }R_U \le r_{ij}
\end{cases} </math>
Therefore the RL and RU parameters only apply to BNS and ST2.
6-site
A 6-site model that combines all the sites of the 4- and 5-site models was developed by Nada and van der Eerden[14]. It was found to reproduce the structure and melting of ice better than other models.
Other
- MB model. A more abstract model resembling the Mercedes-Benz logo that reproduces some features of water in two-dimensional systems. It is not used as such for simulations of "real" (i.e., three-dimensional) systems, but it is useful for qualitative studies and for educational purposes.[15]
- Coarse-grained models. One- and two-site models of water have also been developed.[16]
Computational cost
The computational cost of a water simulation increases with the number of interaction sites in the water model. The CPU time is approximately proportional to the number of interatomic distances that need to be computed. For the 3-site model, 9 distances are required for each pair of water molecules (every atom of one molecule against every atom of the other molecule, or 3 × 3). For the 4-site model, 10 distances are required (every charged site with every charged site, plus the O-O interaction, or 3 × 3 + 1). For the 5-site model, 17 distances are required (4 × 4 + 1). Finally, for the 6-site model, 26 distances are required (5 × 5 + 1).
When using rigid water models in molecular dynamics, there is an additional cost associated with keeping the structure constrained, using constraint algorithms (although with bond lengths constrained it is often possible to increase the time step).
See also
References
- ↑ Jorgensen, W. L. Quantum and statistical mechanical studies of liquids. 10. Transferable intermolecular potential functions for water, alcohols, and ethers. Application to liquid water. J. Am. Chem. Soc. 1981, 103, 335-340.
- ↑ H.J.C. Berendsen, J.P.M. Postma, W.F. van Gunsteren, and J. Hermans, In Intermolecular Forces, edited by B. Pullman (Reidel, Dordrecht, 1981), p. 331.
- ↑ 3.0 3.1 Jorgensen, W. L.; Chandrasekhar, J.; Madura, J.; Impey, R. W.; Klein, M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys 1983, 79, 926-935. doi:10.1063/1.445869
- ↑ H. J. C. Berendsen, J. R. Grigera, and T. P. Straatsma. The Missing Term in Effective Pair Potentials. J. Phys. Chem 1987, 91, 6269-6271. doi:10.1021/j100308a038
- ↑ MacKerell, A. D., Jr.; Bashford, D.; Bellott, R. L.; Dunbrack, R. L., Jr.; Evanseck, J. D.; Field, M. J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; Joseph-McCarthy, D.; Kuchnir, L.; Kuczera, K.; Lau, F. T. K.; Mattos, C.; Michnick, S.; Ngo, T.; Nguyen, D. T.; Prodhom, B.; Reiher, W. E., III; Roux, B.; Schlenkrich, M.; Smith, J. C.; Stote, R.; Straub, J.; Watanabe, M.; Wiorkiewicz-Kuczera, J.; Yin, D.; Karplus, M. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. 1998, 102, 3586-3616. doi:10.1021/jp973084f
- ↑ Bernal, J. D.; Fowler, R.H. J. Chem. Phys. 1933, 1, 515. doi:10.1063/1.1749327
- ↑ Jorgensen, W. L. Revised TIPS for simulations of liquid water and aqueous solutions. J. Chem. Phys 1982, 77, 4156-4163. doi:10.1063/1.444325
- ↑ H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura, and T. Head-Gordon. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004, 120, 9665-9678. doi:10.1063/1.1683075
- ↑ J. L. F. Abascal, E. Sanz, R. García Fernández, and C. Vega. A potential model for the study of ices and amorphous water: TIP4P/Ice. J. Chem. Phys. 2005, 122, 234511. doi:10.1063/1.1931662
- ↑ J. L. F. Abascal and C. Vega. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. doi:10.1063/1.2121687
- ↑ 11.0 11.1 F.H. Stillinger, A. Rahman, Improved simulation of liquid water by molecular dynamics. J. Chem. Phys. 1974, 60, 1545-1557. doi:10.1063/1.1681229
- ↑ Mahoney, M. W.; Jorgensen, W. L. A five-site model liquid water and the reproduction of the density anomaly by rigid, non-polarizable models. J. Chem. Phys. 2000, 112, 8910-8922. doi:10.1063/1.481505
- ↑ Rick, S. W. A reoptimization of the five-site water potential (TIP5P) for use with Ewald sums. J. Chem. Phys. 2004, 120, 6085-6093. doi:10.1063/1.1652434
- ↑ H. Nada, J.P.J.M. van der Eerden, J. Chem. Phys. 2003, 118, 7401. doi:10.1063/1.1562610
- ↑ K. A. T. Silverstein, A. D. J. Haymet, and K. A. Dill. A Simple Model of Water and the Hydrophobic Effect. J. Am. Chem. Soc. 1998, 120, 3166-3175. doi:10.1021/ja973029k
- ↑ S. Izvekov, G. A. Voth. Multiscale coarse graining of liquid-state systems J. Chem. Phys. 2005, 123, 134105. doi:10.1063/1.2038787